Logo

Unveiling the Backbone-Optimizer Coupling Bias in Visual Representation Learning

Siyuan Li1,2*, Juanxi Tian1,*, Zedong Wang1,*, Luyuan Zhang1, Zicheng Liu1,2, Weiyang Jin1, Yang Liu3, Baigui Sun3, Stan Z. Li1,†,
▶ 1AI Lab, Research Center for Industries of the Future, Westlake University, Hangzhou, China ▶ 2Zhejiang University, Hangzhou, China ▶ 2DAMO Academy, Hangzhou, China
*Equal Contribution †Corresponding author
arXiv Code Benchmark
BOCB Image

Abstract

This paper delves into the interplay between vision backbones and optimizers, unvealing an inter-dependent phenomenon termed backbone-optimizer coupling bias (BOCB). We observe that canonical CNNs, such as VGG and ResNet, exhibit a marked co-dependency with SGD families, while recent architectures like ViTs and ConvNeXt share a tight coupling with the adaptive learning rate ones. We further show that BOCB can be introduced by both optimizers and certain backbone designs and may significantly impact the pre-training and downstream fine-tuning of vision models. Through in-depth empirical analysis, we summarize takeaways on recommended optimizers and insights into robust vision backbone architectures. We hope this work can inspire the community to question long-held assumptions on backbones and optimizers, stimulate further explorations, and thereby contribute to more robust vision systems. The source code and models are publicly available.

Model is a complex DNN system, and Coupling Bias to the components of the entire system should be considered when changing microcosmic.

Introduction

🌟[NEW!] We explore the crucial yet poorly studied backbone-optimizer interplay in visual representation learning, revealing the phenomenon of backbone-optimizer coupling bias (BOCB).

🌟[NEW!] We provide the backbone-optimizer benchmark that encompasses 20 popular vision backbones, from classical CNNs to recent transformer-based architectures, and evaluate their performance against 20 mainstream optimizers on CIFAR-100, ImageNet-1K, and COCO, unveiling the practical limitations introduced by BOCB in both pre-training and transfer learning scenarios.

🌟[NEW!] From the BOCB perspective, we summarize optimizers recommendations and insights on more robust vision backbone design. The benchmark results also serve as takeaways for user-friendly deployment. We open-source the code and models for further explorations in the community.

🗣️We hope this work could stimulate further discussions on the relationship between neural networks and optimizers in (visual) representation learning, potentially influence how researchers approach neural network design and optimization in computer vision and even beyond.

🤔As well as discussions on many extended topics, such as whether the long-standing debate between CNNs and Transformers has been settled (especially in an era where model scaling up/down is becoming increasingly important), and whether there are better optimizers that can replace AdamW after years of development, and so on. These topics may find clearer answers following the BOCB.

↓

Q1: Does any identifiable dependency exist between existing vision backbones and widely-used optimizers?

Q2: If such backbone-optimizer dependencies exist, (how) do they affect the training dynamics and performance of vision models?

Q3: Can we identify direct connections between these inter-dependencies and specific designs of vision backbone architectures and optimizers?

Logo

New team & New series work!

A new team, Black-Box Optimization & Coupling Bias (BOCB), has been established by Juanxi Tian, Siyuan Li, and Zedong Wang. We believe that our first work, 'Backbone-Optimizer Coupling Bias' marks a promising start for our team. Moving forward, we will focus on a broader range of scenarios in Deep Learning, exploring more intriguing and even counterintuitive phenomena to better understand the Coupling Bias in complex DL systems. We aim to make significant optimizations and improvements. Stay tuned for more exciting developments.

Visual Insights

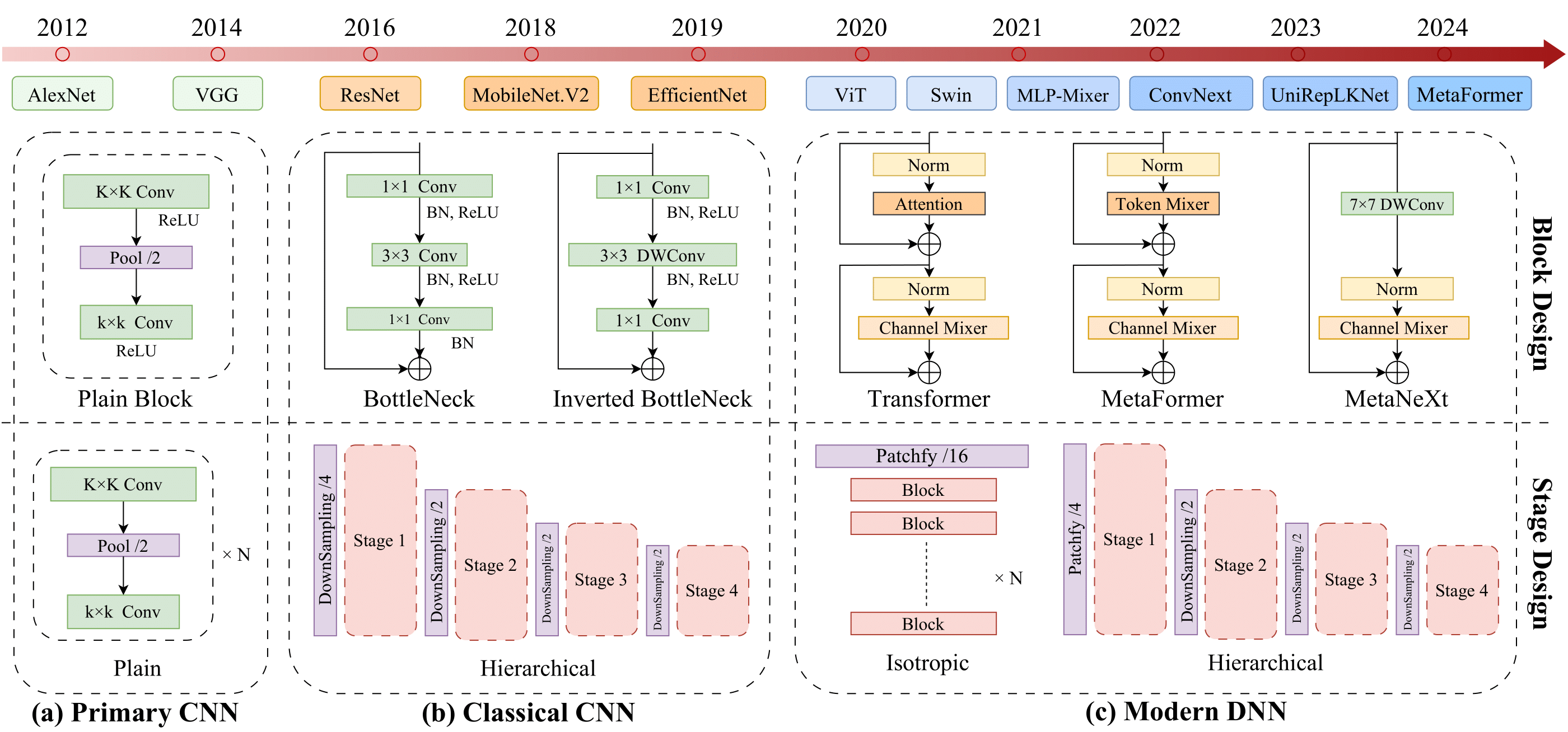
Backbone Roadmap.

Backbone Roadmap

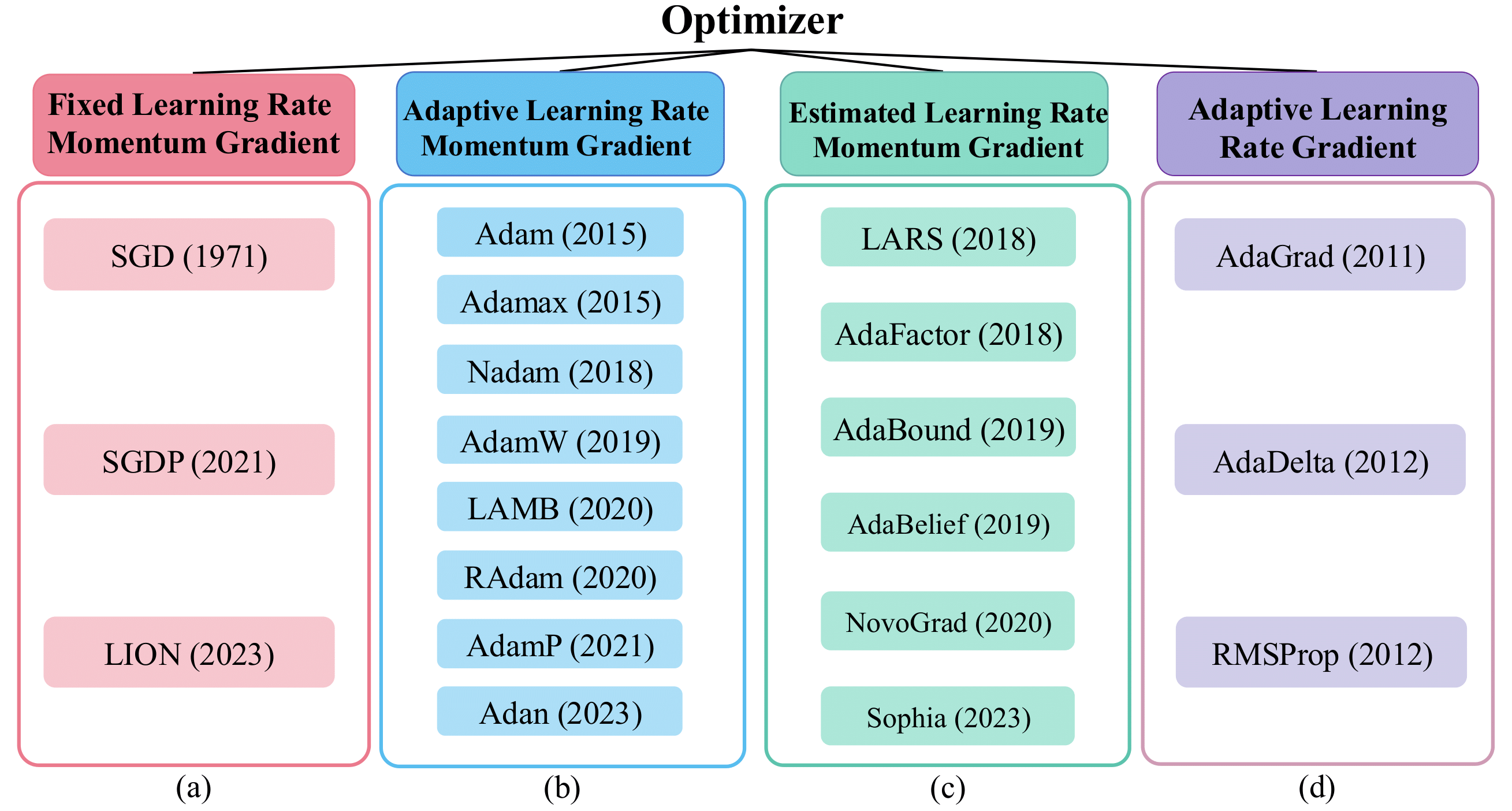
General Algorithm of Optimizer for DNNs.

General Algorithm of Optimizer for DNNs

Four categories optimizer.

Four categories optimizer

Violinplot of the performance stability for different backbones.

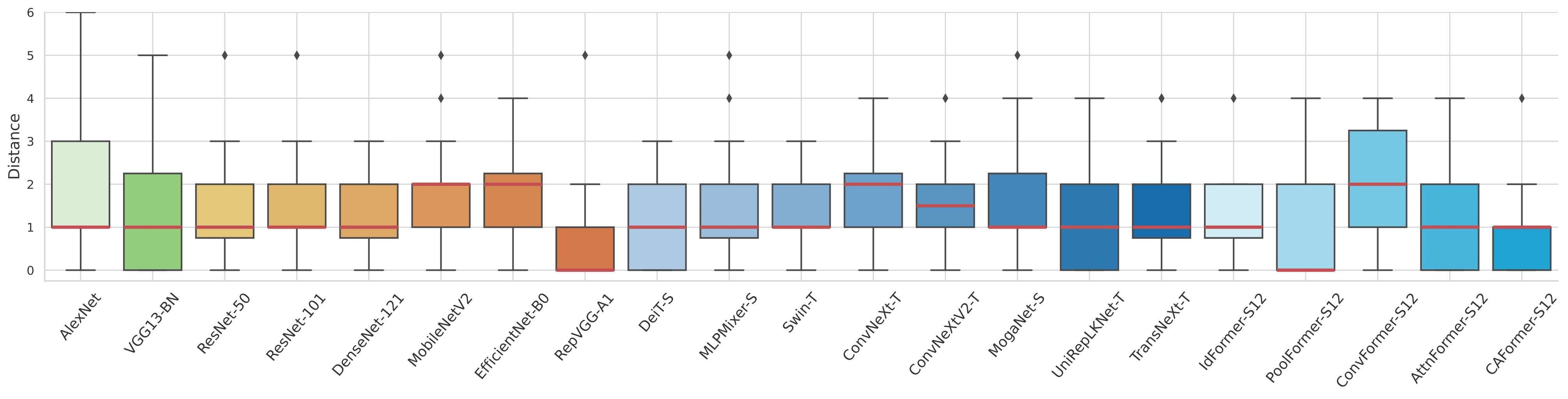
Hyper-parameters consistency

Boxplot visualization of hyper-parameter robustness.

Hyper-parameters consistency

Boxplot of optimizers generality.

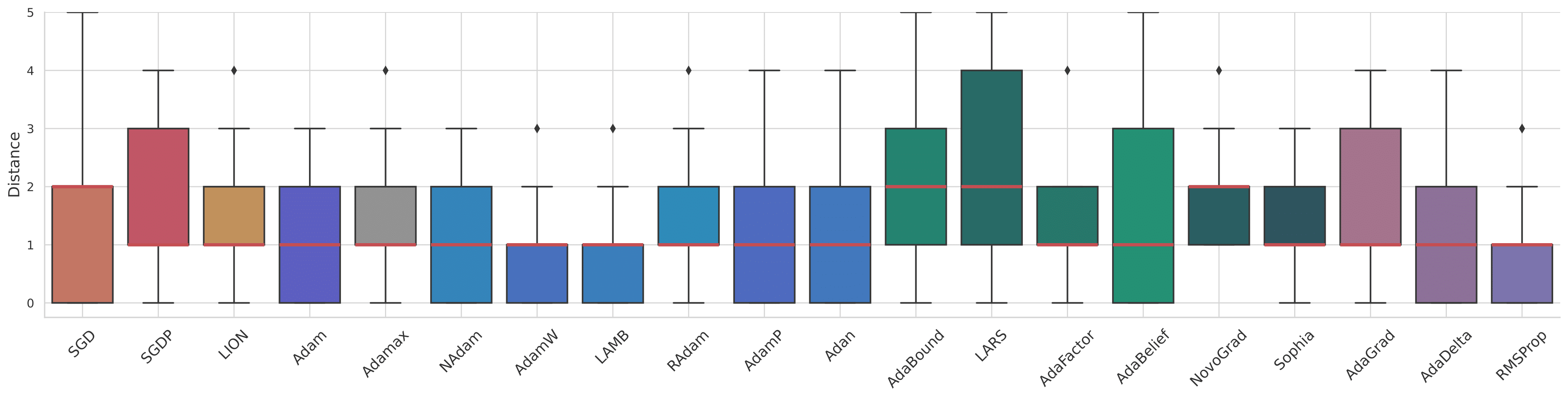
Optimizer generality

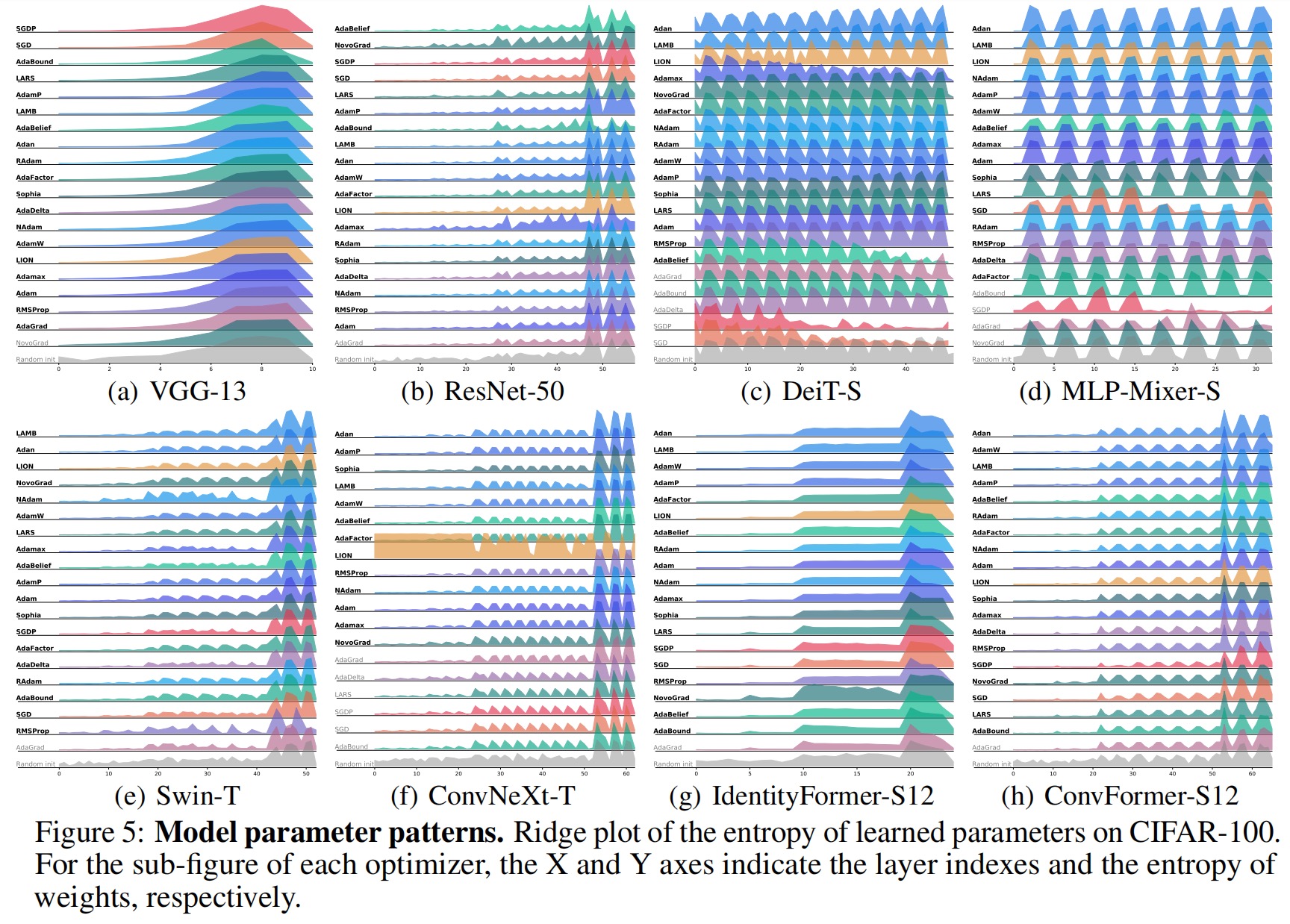
Model parameter patterns.

Model parameter patterns

CIFAR100 Benchmark

Top-1 accuracy (\%) of representative vision backbones with 20 popular optimizers on CIFAR-100. The torch-style training settings are used for AlexNet, VGG-13, R-50 (ResNet-50), DN-121 (DenseNet-121), MobV2 (MobileNet.V2), and RVGG-A1 (RepVGG-A1), while other backbones adopt modern recipes, including Eff-B0 (EfficientNet-B0), ViT variants, ConvNeXt variants (CNX-T and CNXV2-T), Moga-S (MogaNet-S), URLK-T (UniRepLKNet-T), and TNX-T (TransNeXt-T). We list MetaFormer S12 variants apart from other modern DNNs as IF-12, PFV2-12, CF-12, AF-12, and CAF-12.

The blue and gray features denote the top-4 and trivial results, while others are inliers.

Two bottom lines report mean, std, and range on statistics that removed the worst result for all models.

You can swipe left and right to see the full table.

Backbone AlexNet VGG-13 R-50 DN-121 MobV2 Eff-B0 RVGG-A1 DeiT-S MLP-S Swin-T CNX-T CNXV2-T Moga-S URLK-T TNX-T IF-12 PFV2-12 CF-12 AF-12 CAF-12
SGD-M 66.76 77.08 78.76 78.01 77.16 79.41 72.64 75.85 63.20 78.95 60.09 82.25 75.93 82.75 86.21 77.40 77.70 83.46 83.02 81.21
SGDP 66.54 77.56 79.25 78.93 77.32 79.55 75.26 63.53 69.24 80.56 61.25 82.43 80.86 82.18 86.12 77.55 77.53 83.54 82.88 81.56
LION 62.11 73.87 75.28 75.42 74.62 76.97 73.55 74.57 74.19 81.84 82.29 82.53 85.03 83.43 86.96 78.65 79.66 84.62 82.41 79.59
Adam 65.29 73.41 74.55 76.78 74.56 76.48 75.06 71.04 72.84 80.71 82.03 82.66 84.92 84.73 86.23 78.39 79.18 84.81 81.54 82.18
Adamax 67.30 73.80 75.21 73.52 74.60 78.37 74.33 73.31 73.07 81.28 80.25 81.90 84.51 83.81 86.34 78.02 79.55 84.31 81.83 82.50
NAdam 60.49 73.96 74.82 76.10 75.08 77.06 74.86 72.75 73.77 81.80 82.26 82.72 85.23 82.07 86.44 78.37 80.32 84.81 81.82 82.83
AdamW 62.71 73.90 75.56 78.14 76.88 78.77 75.35 72.15 73.59 81.30 83.52 83.59 86.19 86.30 87.51 79.39 80.55 85.46 82.24 83.60
LAMB 66.90 75.55 77.19 78.81 77.59 78.77 77.04 75.39 74.98 83.47 84.13 84.93 86.04 84.99 87.37 80.21 80.01 85.40 83.16 83.74
RAdam 61.69 74.64 75.19 76.40 75.94 77.08 74.83 72.41 72.11 79.84 82.18 82.69 84.95 84.26 86.49 78.46 79.71 84.93 81.44 82.35
AdamP 60.27 75.56 78.17 78.89 77.79 78.65 77.67 71.55 73.66 80.91 84.47 84.40 86.45 86.19 87.16 79.20 81.70 85.15 82.12 83.40
Adan 63.98 74.90 77.08 79.33 77.73 78.43 76.99 76.33 74.94 83.35 84.65 84.77 86.46 86.75 87.47 80.59 83.23 85.58 83.51 84.89
AdaBound 66.59 77.00 78.11 75.26 78.76 79.88 74.14 68.59 70.31 80.67 71.96 83.90 78.48 83.03 86.07 77.99 77.81 82.73 83.08 82.38
LARS 64.35 75.71 78.25 77.25 76.23 72.43 75.50 71.36 72.64 81.29 61.40 82.22 33.26 41.03 85.16 77.66 78.78 82.98 81.00 82.05
AdaFactor 63.91 74.49 75.41 77.03 75.38 77.83 75.03 74.02 71.16 80.36 82.82 83.06 85.17 85.99 86.57 78.78 78.81 84.90 81.94 82.36
AdaBelief 62.98 75.09 80.53 79.26 75.78 78.48 76.90 70.66 73.30 80.98 83.31 84.47 84.80 84.54 86.64 78.55 81.01 85.03 83.21 83.56
NovoGrad 64.24 76.09 79.36 77.25 71.26 74.23 75.16 73.13 67.03 81.82 79.99 82.01 82.96 80.77 85.85 77.16 78.92 83.51 81.28 82.98
Sophia 64.30 74.18 75.19 77.91 76.60 78.95 75.85 71.47 72.74 80.61 83.76 83.94 85.39 84.20 86.60 77.67 78.90 84.58 81.67 82.96
AdaGrad 45.79 71.29 73.30 51.70 33.87 77.93 46.06 67.24 67.50 75.83 75.63 50.34 83.03 82.57 66.83 44.34 44.40 79.67 78.71 38.09
AdaDelta 66.87 74.14 75.07 76.82 75.32 77.88 74.58 65.44 71.32 80.25 74.25 82.74 81.06 84.17 85.31 75.91 76.40 84.05 82.62 82.08
RMSProp 59.33 73.30 74.25 75.45 73.94 76.83 74.92 70.71 71.63 77.52 82.29 82.11 85.17 61.14 86.21 77.40 77.14 84.01 79.72 81.83
Mean 63.67 74.68 76.31 76.94 75.65 77.77 75.19 70.82 72.10 80.63 78.13 82.92 83.51 82.40 86.34 78.03 78.94 84.28 81.99 82.32
Std/Range 1.1/8 1.0/4 1.6/6 1.4/6 1.6/8 1.2/6 0.9/4 2.9/13 1.7/8 1.1/6 8.0/25 0.8/3 2.8/11 5.5/26 0.6/2 0.8/5 1.2/7 0.8/3 0.9/4 0.9/5

Transfer Learning to Object Detection and 2D Pose Estimation

Transfer learning to object detection (Det.) with RetinaNet and 2D pose estimation (Pose.) with TopDown on COCO, evaluated by mAP (%) and AP$^{50}$ (%). We employ pre-trained VGG, ResNet-50 (R-50), Swin-T, and ConvNeXt-T (CX-T) with different pre-training settings, where 100-epoch pre-train by SGD, LARS, or RSB A3 (LAMB), 300-epoch pre-train by AdamW, Adan or RSB A2 (LAMB), and 600-epoch pre-train with RSB A1 (LAMB).

Pre-training 2D Pose Estimation Object Detection
VGG (SGD) R-50 (SGD) Swin-T (AdamW) R-50 (SGD) R-50 (LARS) R-50 (A3) R-50 (A2) R-50 (A1) R-50 (Adan) Swin-T (AdamW) CX-T (AdamW)
SGD-M 47.5 71.6 38.4 36.6 27.5 28.7 23.7 34.6 27.5 37.2 38.5
SGDP 47.3 41.2 38.9 36.6 17.6 18.5 26.8 26.7 27.4 37.2 22.5
LION 69.5 71.5 71.3 32.1 35.8 35.4 37.6 34.6 38.8 41.9 42.8
Adam 69.8 71.6 72.7 36.2 36.2 35.8 38.3 38.4 38.6 41.9 43.1
Adamax 69.0 71.2 72.4 36.8 36.8 36.4 38.3 38.4 38.3 41.5 42.0
NAdam 69.7 71.8 71.9 36.0 36.6 36.1 38.2 38.4 38.7 41.9 43.4
AdamW 70.0 72.0 72.8 37.1 37.1 36.7 38.4 39.5 36.8 41.8 43.4
LAMB 68.5 71.5 71.7 36.7 37.5 37.7 38.6 38.9 38.6 41.8 42.6
RAdam 69.8 71.8 72.6 36.6 36.5 36.0 38.2 38.4 38.6 41.6 43.3
AdamP 69.7 71.5 72.8 36.5 37.2 36.5 38.5 38.9 38.8 41.7 43.3
Adan 69.7 72.1 72.8 37.7 37.0 36.0 38.6 39.0 39.4 42.0 43.2
AdaBound 34.0 44.9 28.4 35.9 34.2 31.9 37.0 35.0 36.7 38.8 41.2
LARS 54.4 63.4 47.6 35.8 28.9 28.8 34.7 36.9 37.3 34.6 40.5
AdaFactor 72.8 71.7 72.7 35.6 37.0 36.4 38.5 37.8 38.7 40.5 43.1
AdaBelief 69.6 67.0 61.8 36.2 34.4 33.1 36.4 38.2 38.5 40.0 41.4
NovoGrad 64.2 70.7 69.8 35.6 27.2 26.3 35.2 28.6 38.5 40.4 39.0
Sophia 69.7 71.6 72.3 36.4 35.8 35.3 38.0 38.7 37.0 40.4 42.5
AdaGrad 66.0 61.2 48.4 26.4 21.9 28.3 32.7 27.1 33.7 32.9 23.7
AdaDelta 44.3 49.3 52.0 34.9 32.7 32.7 35.9 33.9 36.6 40.0 41.5
RMSProp 68.8 71.6 72.5 35.3 36.2 35.6 37.8 38.3 38.7 41.5 43.1

ImageNet-1K Benchmark

Top-1 accuracy (%) of DeiT-S and ResNet-50 training 300 epochs by popular optimizers using DeiT and RSB A2 training recipes on ImageNet-1K.

Backbone DeiT-S (DeiT) R-50 (A2)
SGD-M 75.35 78.82
SGDP 76.34 78.02
LION 78.78 78.92
Adam 78.44 78.16
Adamax 77.71 78.05
NAdam 78.26 78.97
AdamW 80.38 79.88
LAMB 80.23 79.84
RAdam 78.54 78.75
AdamP 79.26 79.28
Adan 80.81 79.91
AdaBound 72.96 75.37
LARS 73.18 79.66
AdaFactor 79.98 79.36
AdaBelief 75.32 78.25
NovoGrad 71.26 76.83
Sophia 79.65 79.13
AdaGrad 54.96 74.92
AdaDelta 74.14 77.40
RMSProp 78.03 78.04

Implementation Details (Vision Backbones)

Three categories of typical vision backbones proposed in the past decade.
Backbone Date Stage-wise design Block-wise design Operator (feature extractor) Residual branch Input size Training setting
AlexNet NIPS'2012 - Plain Conv - 224 PyTorch
VGG-13 ICLR'2015 - Plain - Conv - 224 PyTorch
ResNet CVPR'2016 Hierarchical Bottleneck Conv Addition 32 PyTorch
DenseNet CVPR'2017 Hierarchical Bottleneck Conv Concatenation 32 PyTorch
MobileNet.V2 CVPR'2018 Hierarchical Inv-bottleneck SepConv Addition 224 PyTorch
EfficientNet ICML'2019 Hierarchical Inv-bottleneck Conv & SE Addition 224 RSB A2
RepVGG CVPR'2021 Hierarchical Inv-bottleneck Conv Addition 224 PyTorch
DeiT-S (ViT) ICML'2021 Patchfy & Isotropic Metaformer Attention PreNorm 224 DeiT
MLP-Mixer-S NIPS'2021 Patchfy & Isotropic Metaformer MLP PreNorm 224 DeiT
Swin Transformer ICCV'2021 Patchfy & Hierarchical Metaformer Local Attention PreNorm 224 ConvNeXt
ConvNeXt CVPR'2022 Patchfy & Hierarchical MetaNeXt DWConv PreNorm & LayerScale 32 ConvNeXt
ConvNeXt.V2 CVPR'2023 Patchfy & Hierarchical MetaNeXt DWConv PreNorm & LayerScale 32 ConvNeXt
MogaNet ICLR'2024 Patchfy & Hierarchical Metaformer DWConv & Gating PreNorm & LayerScale 32 ConvNeXt
UniRepLKNet CVPR'2024 Patchfy & Hierarchical Metaformer DWConv & SE PreNorm & LayerScale 224 ConvNeXt
TransNeXt CVPR'2024 Patchfy & Hierarchical Metaformer Attention & Gating PreNorm & LayerScale 224 DeiT
IdentityFormer TPAMI'2024 Patchfy & Hierarchical Metaformer Identity PreNorm & ResScale 224 RSB A2
PoolFormerV2 TPAMI'2024 Patchfy & Hierarchical Metaformer Pooling PreNorm & ResScale 224 RSB A2
ConvFormer TPAMI'2024 Patchfy & Hierarchical Metaformer SepConv PreNorm & ResScale 224 RSB A2
AttentionFormer TPAMI'2024 Patchfy & Hierarchical Metaformer Attention PreNorm & ResScale 224 RSB A2
CAFormer TPAMI'2024 Patchfy & Hierarchical Metaformer SepConv & Attention PreNorm & ResScale 224 RSB A2

Implementation Details (Optimizer)

.
Four categories of typical optimizers with their components. From top to bottom are (a) fixed learning rate with momentum gradient, (b) adaptive learning rate with momentum gradient, (c) estimated learning rate with momentum gradient, and (d) adaptive learning rate with current gradient
Optimizer Date Learning rate Gradient Weight decay
SGD-M TSMC'1971 Fixed lr Momentum ✓
SGDP ICLR'2021 Fixed lr Momentum Decoupled
LION NIPS'2023 Fixed lr Sign Momentum Decoupled
Adam ICLR'2015 Estimated second moment Momentum ✓
Adamax ICLR'2015 Estimated second moment Momentum ✓
AdamW ICLR'2019 Estimated second moment Momentum Decoupled
AdamP ICLR'2021 Estimated second moment Momentum Decoupled
LAMB ICLR'2020 Estimated second moment Momentum Decoupled
NAdam ICLR'2018 Estimated second moment Nesterov Momentum ✓
RAdam ICLR'2020 Estimated second moment Momentum Decoupled
Adan TPAMI'2023 Estimated second moment Nesterov Momentum Decoupled
AdaBelief NIPS'2019 Estimated second moment variance Momentum Decoupled
AdaBound ICLR'2019 Estimated second moment Momentum Decoupled
AdaFactor ICML'2018 Estimated second moment (decomposition) Momentum Decoupled
LARS ICLR'2018 L2-norm of Gradient Momentum Decoupled
Novograd arXiv'2020 Sum of estimated second momentum Momentum Decoupled
Sophia arXiv'2023 Parameter-based estimator Sign Momentum Decoupled
AdaGrad JMLR'2011 Second moment Gradient ✓
AdaDelta arXiv'2012 Estimated second moment param moment Gradient ✓
RMSProp arXiv'2012 Estimated second moment Gradient ✓

Possible impact of BOCB & Insights

The phenomenon of backbone-optimizer coupling bias (BOCB) we observed during the benchmarking arises from the intricate interplay between the design principles of vision backbones and the inherent properties of optimizers. In particular, we notice that traditional CNNs, such as VGG and ResNets, exhibit a marked coupling with SGD optimizers. In contrast, modern meta-architectures like ViTs and ConvNeXt strongly correlate with adaptive learning rate optimizers, particularly AdamW. As aforementioned, we assume that such a coupling bias may stem from the increasing complexity of optimization as backbone architectures evolve. Concretely, recent backbones incorporate complex elements such as stage-wise hierarchical structures, advanced token-mixers, and block-wise heterogeneous structures. These designs shape a more intricate and challenging optimization landscape, necessitating adaptive learning rate strategies and effective momentum handling. Thus, modern backbones exhibit stronger couplings with optimizers that can navigate these complex landscapes. The BOCB phenomenon has several implications for the design and deployment of vision backbones:

  • (A) Deployment: Vision backbones with weaker BOCB offer greater flexibility and are more user-friendly, especially for practitioners with limited resources for extensive hyper-parameter tuning. However, modern architectures like ViTs and ConvNeXt, which exhibit strong coupling with adaptive optimizers, require careful optimizer selection and hyper-parameter tuning for optimal performance.
  • (B) Backbone Design Insights: While weaker coupling offers more user-friendliness, stronger coupling can potentially lead to better performance and generalization. Tailoring the optimization process to certain architectural characteristics of modern backbones, such as stage-wise hierarchical structures and attention mechanisms for token mixing, can more effectively navigate complex optimization landscapes, unlocking superior performance and generalization capabilities.
  • (C) Design Principles: The observed BOCB phenomenon highlights the need to consider the coupling between backbone designs and optimizer choices. When designing new backbone architectures, it is crucial to account for both the inductive bias (e.g., hierarchical structures and local operations) and some optimizing auxiliary modules introduced by the macro design principles. A balanced approach that harmonizes the backbone design with the appropriate optimizer choice can lead to optimal performance and efficient optimization, enabling the full potential of the proposed architecture to be realized.

Origins of BOCB: Backbone Macro Design and Token Mixers

To investigate the causes of BOCB, we first consider what matters the most: optimizers or backbones. As shown in Figure 4 and Table 1, four categories of optimizers show different extents of BOCB with vision backbones. Category (a) shows a broader performance dispersion, necessitating meticulous hyper-parameter tuning to classical CNNs while demonstrating less adaptability to advanced backbones' optimization demands. Category (b) and Category (c) exhibit a robust, hyperparameter-insensitive performance peak, adept at navigating the complex optimization landscapes of primary CNNs and modern DNNs. Category (d) shows the worst performances and heavy BOCB. The trajectory of vision backbone macro design has significantly sculpted the optimization landscape, progressing through distinct phases that reflect the intricate relationship between network architectural complexity and training challenges.

  • Early-stage CNNs: These architectures featured a straightforward design of plainly stacked convolutional and pooling layers, culminated by fully connected layers. Such a paradigm was effective but set the stage for further optimization of landscape alterations.
  • Classical CNNs: The introduction of ResNet marked a pivotal shift towards stage-wise hierarchical designs, significantly enhancing feature extraction and representation learning ability. ResNet-50, in particular, demonstrated a well-balanced approach to BOCB, which exhibited strong compatibility with SGD optimizers and a relatively lower BOCB compared to its contemporaries.
  • Modern Architectures: The transition to modern backbones introduced simplified block-wise designs (e.g., MetaNeXt) and ConvNeXt variants, ConvNeXtV2, or complex block-wise heterogeneous structures (e.g., MogaNet and UniRepLKNet), increasing the optimization challenge and the degree of BOCB due to their complex feature extraction. Representing a pinnacle in evolution, the MetaFormer architecture incorporates both stage-wise and block-wise heterogeneity into its design. This innovative macro design refines the optimization landscape by harmonizing with optimizers, leading to reduced BOCB and enhanced performance.

For details, please refer to the full paper.

BibTeX


@misc{li2024unveilingbackboneoptimizercouplingbias,
    title={Unveiling the Backbone-Optimizer Coupling Bias in Visual Representation Learning}, 
    author={Siyuan Li and Juanxi Tian and Zedong Wang and Luyuan Zhang and Zicheng Liu and Weiyang Jin and Yang Liu and Baigui Sun and Stan Z. Li},
    year={2024},
    eprint={2410.06373},
    archivePrefix={arXiv},
    primaryClass={cs.CV},
    url={https://arxiv.org/abs/2410.06373}, 
}

Contribution

Juanxi Tian @Juanxi Tian
Siyuan Li @Siyuan Li
Zedong Wang @Zedong Wang

Acknowledgement

We sincerely thank Zhuang Liu for the insightful discussions and valuable suggestions. This research was primarily conducted by Siyuan Li, Juanxi Tian, and Zedong Wang.

© 2024 BOCB. All rights reserved.